VBA 回帰式を用いて多数のデータを生成する - PythonとVBAで世の中を便利にする

本記事は、実機評価もしくはシミューレーション等で得られたデータ分析ですでに回帰式が得られている場合に関する。本プログラムは、VBAで乱数を生成して、その乱数を回帰式へ代入計算して多数のデータを生成する。そのため、設計段階のマージン検証などに使える。

本プログラム実行前のエクセルシートのフォーマットを下図に示す。2行目のB列には予め手入力しておく必要がある。

f:id:HK29:20180311231858p:plain

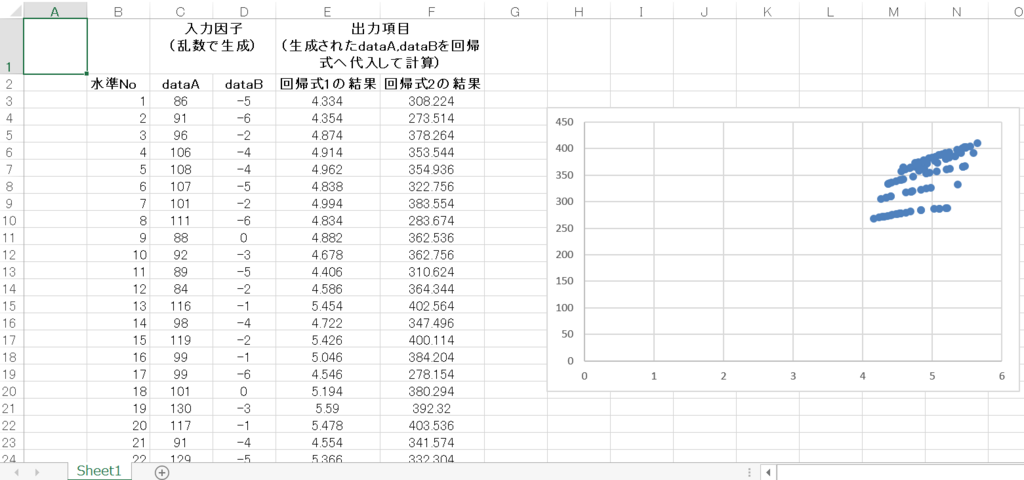
実行後の状態を下図に示す。C,D列に回帰式へ入力する因子dataA,dataBを乱数(Rnd関数)で生成する。そして、出力項目は2つありE,F列である。回帰式が二つあるのは、異なる目的変数二つに対する回帰式であり、次の二つである。

ある目的変数1に対する回帰式1＝A_segm＋dataA×A_coef1＋dataB×A_coef2

ある目的変数2に対する回帰式2＝B_segm＋dataA×B_coef1＋dataB×B_coef2＋dataA×dataA×B_coef3＋dataB×dataB×B_coef4＋dataA×dataB×B_coef5

ちなみに、下図右は横軸に回帰式1、縦軸に回帰式2の結果をプロットしたグラフである。

f:id:HK29:20180311232036p:plain

▼本プログラム

Sub モンテカルロ()
Dim myColum, myStartRow As Integer
Dim A_min, A_range, B_min, B_range As Integer
Dim A_segm, A_coef1, A_coef2, A_coef3, A_coef4, A_coef5 As Double
Dim B_segm, B_coef1, B_coef2, B_coef3, B_coef4, B_coef5 As Double

Dim N, i, k As Integer
Dim dataA, dataB As Integer
'------------------------------------------------パラメータ
'実行回数
N = 100

'データ入力のセル行列
myColum = 2
myStartRow = Cells(Rows.Count, myColum).End(xlUp).Row

'乱数の生成範囲
A_min = 80
A_range = 50 + 1

B_min = 0
B_range = 6 + 1

'-----回帰係数------
'回帰式1
A_segm = 2.77      '切片
A_coef1 = 0.024    '一次の項
A_coef2 = 0.1      '一次の項
A_coef3 = 0        '二次の項
A_coef4 = 0        '二次の項
A_coef5 = 0        '交互の項

'回帰式2
B_segm = 189
B_coef1 = 2.5
B_coef2 = -24
B_coef3 = -0.006
B_coef4 = -4.62
B_coef5 = 0.13
'------------------------------------------------

i = 1
k = myStartRow + i
Do While i <= N
    Cells(k, myColum) = i
    '▼乱数生成（入力因子dataA）
    'Rnd関数で0～1未満の乱数が生成される
    'A_rangeの(50+1)との積で、0～51未満の範囲となり、int関数で0～50となる
    'A_minの80との和で、生成される乱数は80～130となる。
    Cells(k, myColum + 1) = A_min + Int(A_range * Rnd)

    '▼乱数生成（入力因子dataB）
    'マイナスの範囲の乱数としたい場合の例
    Cells(k, myColum + 2) = B_min + Int(B_range * Rnd) * (-1)

    dataA = Cells(k, myColum + 1)
    dataB = Cells(k, myColum + 2)
    Cells(k, myColum + 3) = A_segm + dataA * A_coef1 + dataB * A_coef2 + _
                               dataA * dataA * A_coef3 + dataB * dataB * A_coef4 + _
                               dataA * dataB * A_coef5
    Cells(k, myColum + 4) = B_segm + dataA * B_coef1 + dataB * B_coef2 + _
                               dataA * dataA * B_coef3 + dataB * dataB * B_coef4 + _
                               dataA * dataB * B_coef5
    i = i + 1
    k = myStartRow + i
Loop
End Sub

以上

<広告>

リンク