Python 二変数関数の等高線図、3D図を描画する方法

'20/08/10更新：記事とコードを若干編集しました。

　本記事では、2つの方法について雛形コードを載せました。
■1. numpyのndarray型の「二重配列」でデータセットしてグラフ化する方法
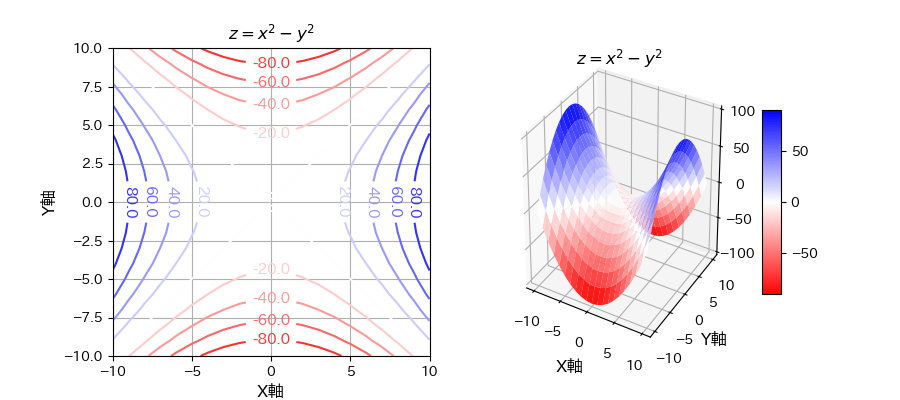
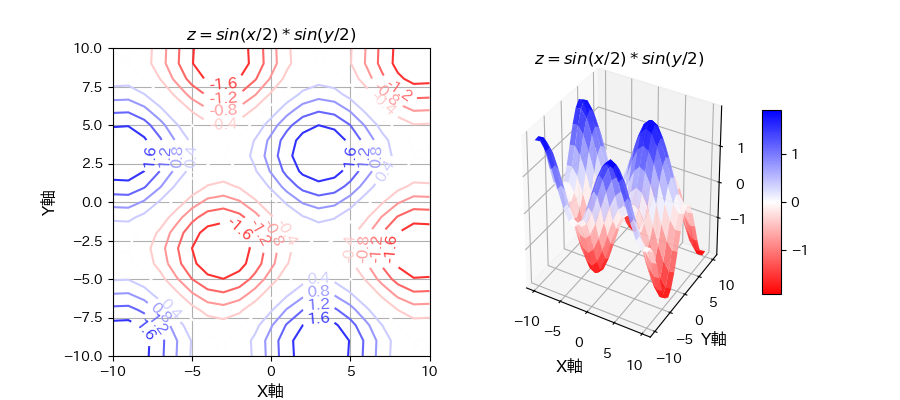
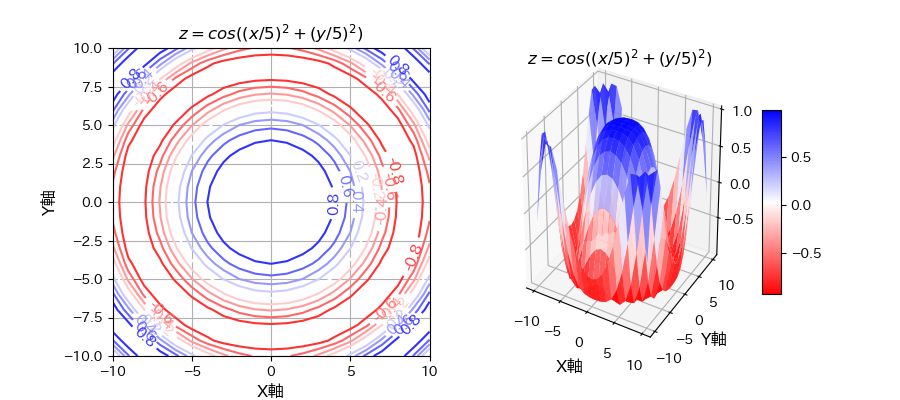
二変数関数について、等高線図と三次元図を描画した例が下図5つです。

■2. numpyのndarray型の「一次元配列」でデータセットしてグラフ化する方法
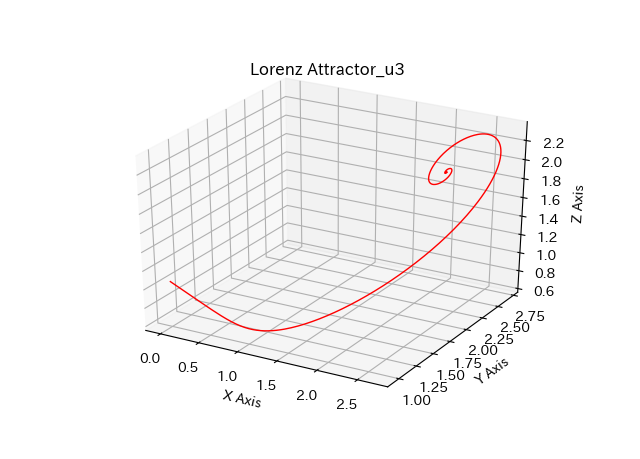
ローレンツ方程式（常微分方程式）を三次元描画した例が下図3つです。

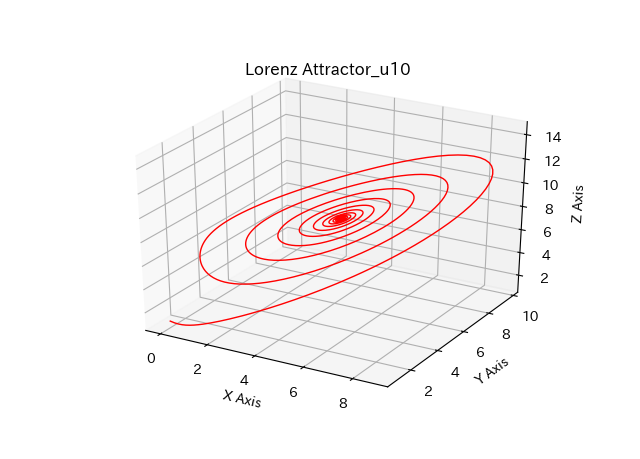
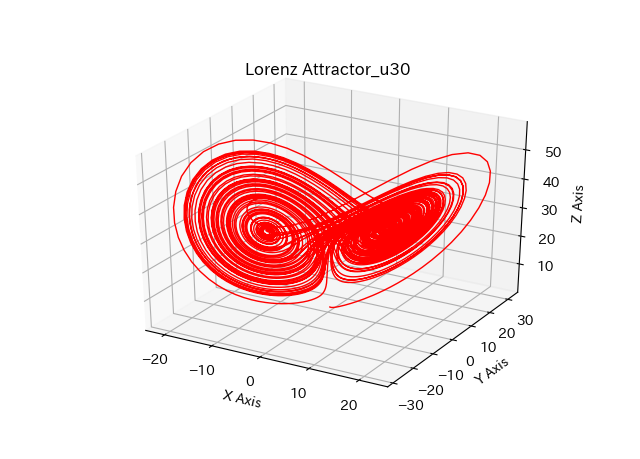
■本プログラム

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib
#matplotlib.use('Agg')
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import seaborn as sns
# 日本語表示したい場合は下記コマンドでインストールし、インポートする
# pip install japanize-matplotlib
#import japanize_matplotlib

import datetime
now = datetime.datetime.now()
now = now.strftime("%y%m%d")

def my_funcA(x, y):
    return 6 * x - pow(x, 2) + 4 * y - pow(y, 2)

def my_funcB(x, y):
    return pow(x, 2) - pow(y, 2)

def my_funcC(x, y):
    return x*(np.exp(-1 * pow(x/5, 2) - pow(y/5, 2)))

def my_funcD(x, y):
    return np.sin(x/2) + np.sin(y/2)

def my_funcE(x, y):
    return np.cos(pow(x/5, 2) + pow(y/5, 2))

def my_lorenz(x, y, z, a=10, b=8/3, u=1):
    x_dot = -a * x + a * y
    y_dot = u * x - y - x * z
    z_dot = -b * z + x * y
    
    return x_dot, y_dot, z_dot


### 等高線図と3D図の作成例1：ジャグ配列のndarryをグラフセットする場合の関数
def my_contur_and_3Dgraph(X, Y, Z, function_name):
    print('X -> ' + str(X) + '\n' + str(type(X)))
    print('Y -> ' + str(Y) + '\n' + str(type(Y)))
    print('Z -> ' + str(Z) + '\n' + str(type(Z)))
    
    fig = plt.figure(figsize=(9, 4))

    # 等高線
    ax1 = fig.add_subplot(121, facecolor="w")
    contour = ax1.contour(X, Y, Z, levels=10, cmap="bwr_r")
    contour.clabel(fmt='%1.1f', fontsize=11)
    # オプション
    ax1.set_title(function_name)
    ax1.set_xlabel(my_xlabel, fontsize=12)
    ax1.set_ylabel(my_ylabel, fontsize=12)
    plt.grid()
    print(type(contour))  # <class 'matplotlib.contour.QuadContourSet'>

    # 3D図
    ax2 = fig.add_subplot(122, projection="3d", facecolor="w")
    surf = ax2.plot_surface(X, Y, Z, cmap="bwr_r", alpha=0.9, cstride=1, rstride=1, lw=0.1)
    # オプション
    fig.colorbar(surf, shrink=0.6, aspect=10) # カラーバー追加。surfでcmapを指定必要
    ax2.set_title(function_name)
    ax2.set_xlabel(my_xlabel, fontsize=12)
    ax2.set_ylabel(my_ylabel, fontsize=12)

    # 作図の実行
    #fig.savefig(now + '_' + function_name + "_contour.png")
    plt.show()
    plt.close()


### 3D図の作成例2：一次元配列のndarryをグラフセットする場合の関数
def my_3Dgraph(X, Y, Z, function_name , u):
    print('X -> ' + str(X) + '\n' + str(type(X)))
    print('Y -> ' + str(Y) + '\n' + str(type(Y)))
    print('Z -> ' + str(Z) + '\n' + str(type(Z)))
    
    fig = plt.figure()
    ax = fig.gca(projection='3d')
    # オプション
    ax.plot(X, Y, Z, color="red", lw=1)
    ax.set_xlabel("X Axis")
    ax.set_ylabel("Y Axis")
    ax.set_zlabel("Z Axis")
    ax.set_title(function_name + '_u' + str(u))

    # 作図の実行
    #fig.savefig(now + '_' + function_name + '_u' + str(u) + "_3D.png")
    plt.show()
    plt.close()


if __name__ == "__main__":
    my_xlabel = 'X軸'
    my_ylabel = 'Y軸'

    ########### 等高線図と3D図の作成例1：ジャグ配列のndarryをグラフセットする場合
    # X, Yを作成
    # np.mgrid[x開始点:x終点:y交差, y開始点:y終点:y公差]
    X, Y = np.mgrid[-10:11:1, -10:11:1]

    Z = my_funcA(X, Y) # 関数A
    my_contur_and_3Dgraph(X, Y, Z, "$z = 6x - x^2 + 4y - y^2$")
    Z = my_funcB(X, Y) # 関数B
    my_contur_and_3Dgraph(X, Y, Z, "$z = x^2 - y^2$")
    Z = my_funcC(X, Y) # 関数C
    my_contur_and_3Dgraph(X, Y, Z, "$z = x(exp(-(x/5)^2 - (y/5)^2))$")
    Z = my_funcD(X, Y) # 関数D
    my_contur_and_3Dgraph(X, Y, Z, "$z = sin(x/2)*sin(y/2)$")
    Z = my_funcE(X, Y) # 関数E
    my_contur_and_3Dgraph(X, Y, Z, "$z = cos((x/5)^2 + (y/5)^2)$")

    ########### 3D図の作成例2：一次元配列のndarryをグラフセットする場合
    # ローレンツ方程式
    dt = 0.01
    num_steps = 10000
    # numpyのndarrayの空セット
    xs = np.empty(num_steps + 1)
    ys = np.empty(num_steps + 1)
    zs = np.empty(num_steps + 1)
    # 初期値のセット
    xs[0], ys[0], zs[0] = (0., 1., 1.05)

    u_list = [1,3,10,30,50]
    for my_u in u_list:
        for i in range(num_steps):
            x_dot, y_dot, z_dot = my_lorenz(xs[i], ys[i], zs[i], a=10, b=8/3, u=my_u)
            xs[i + 1] = xs[i] + (x_dot * dt)
            ys[i + 1] = ys[i] + (y_dot * dt)
            zs[i + 1] = zs[i] + (z_dot * dt)
        my_3Dgraph(xs, ys, zs, "Lorenz Attractor", my_u)

    print('finished')
    

（補足）いずれの場合もnumpy配列を使用するため、数学関数を使用する場合もnumpyを使用することです。そうでない場合は、次のようなエラーが出ます。
TypeError: only size-1 arrays can be converted to Python scalars

以上

<広告>

リンク