リカレントニューラルネットワーク,RNN(Recurrent Neural Network)は、日本語で再帰型ニューラルネットワークと呼び、時系列データのパターン認識、例えば、自然言語応答処理、株価予測などに活用されます。
本記事では、株価予測を例題に雛形コードを載せてます。本家のチュートリアルhttps://www.tensorflow.org/tutorials/structured_data/time_seriesを元にモデルの設定やグラフの見栄え、ハイパーパラメータを株価用に適度に調整しています。
RNNには拡張版がいくつかあり、中でもLSTM(Long Short Term Memory )が主流で長期的な学習に幾分向いているとされます。簡単には、過去データを活用して学習するにあたり、他のNNのようにドロップアウトで過学習を抑制するのではなく、tanhとhard_sigmoid関数を挟むことで適度に学習を進展させます。これにより、単なるRNNのようにすぐに学習しなくなることを防止する試みです。
本記事では5日移動平均のデータを用いて、20日分を予測するコード例です。移動平均の計算は例えば、Python 株価データの欠損値をその前後の値で補完後、単純移動平均を算出する「pandas」 - PythonとVBAで世の中を便利にするで株価のcsvファイルを生成します。
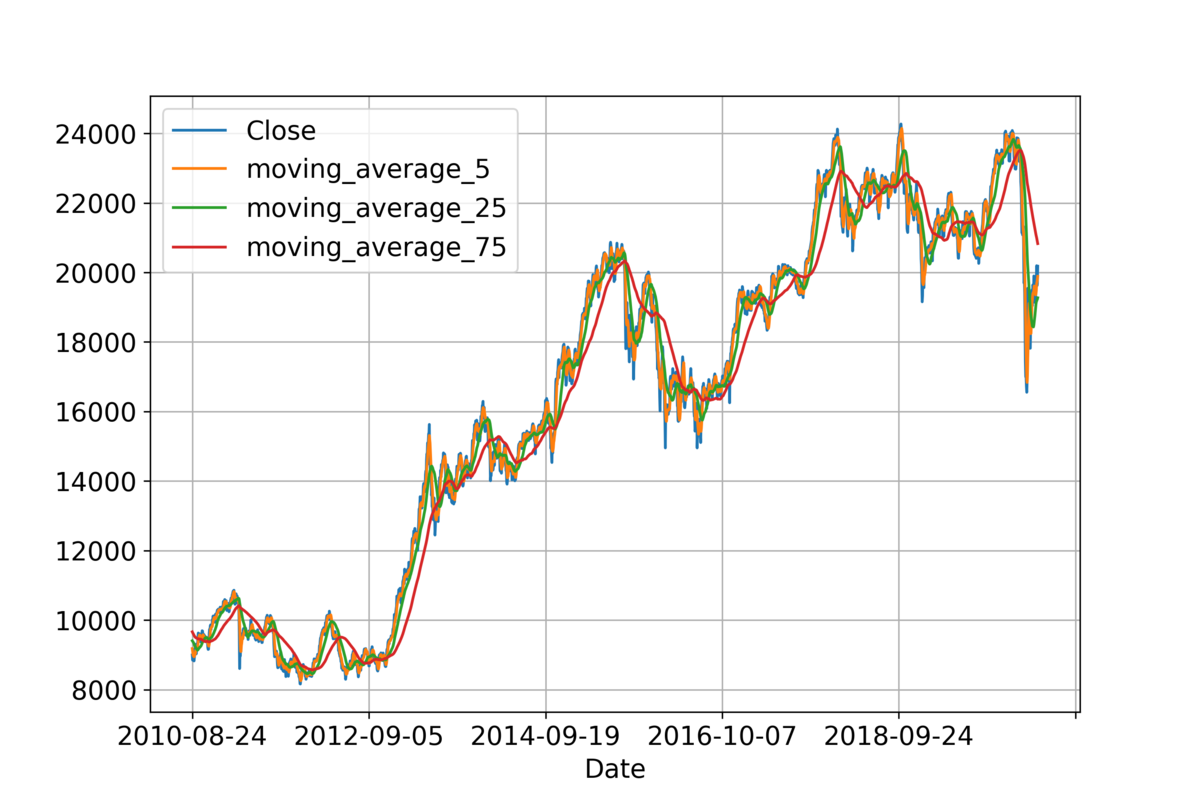
下図にある移動平均5日間のデータを活用した例を示します。本コードではこれに限定せず、objective_feature_index でいずれかを指定できます。
下図は、単変量解析の過程です。横時は学習の世代で、縦軸は損失関数とした平均絶対誤差です。右にゆく程小さい値で学習してる様子がわかります。

下図はバリデーション結果のひとつです。赤×は実データで緑●は予測結果です。絶対値は兎も角、株価が上昇することは的中しました。

下図は、バリデーションサンプル2つ目です。これも上昇することは的中してます。

下図は3つ目の例です。実データの赤×はほぼ株価が変動してないのに対して、予測結果●緑は500円程上昇しており、予測は外れています。

次に、下図は多変量解析の結果です。これも右へゆくほど、学習してる様子がわかります。

下図は、バリデーションデータによる結果のひとつです。青点は実データで、赤点が予測結果です。20日分の多変量予測です。株価が上昇する様子が的中しています。

下図は、バリデーションサンプル2つ目です。これも上昇することは的中してます。

下図は、3つ目の例です。青点は下がっているのに対して、赤点は上昇していてます。つまり、予測結果は外しました。

やってみればわかりますが、ニューラルネットワークは、データ点数が多く必要なだけでなく、データ分析する範囲や、データの前処理、ハイパーパラメータの影響が高いです。非線形問題を解く可能性がある手法であるだけで、それを活用するのは簡単ではないです。
■本プログラム
#!/usr/bin/env python3 # coding: utf-8 # "https://www.tensorflow.org/tutorials/structured_data/time_series" # https://www.tensorflow.org/api_docs/python/tf/keras/layers/BatchNormalization import tensorflow as tf import matplotlib as mpl import matplotlib.pyplot as plt import numpy as np import os import pandas as pd import datetime now = datetime.datetime.now() now = now.strftime("%y%m%d_") mpl.rcParams['figure.figsize'] = (9, 6) mpl.rcParams.update({'font.size': 14}) mpl.rcParams['axes.grid'] = True def multivariate_data(dataset, target, start_index, end_index, history_size, target_size, step, single_step=False): data = [] labels = [] targets = [] start_index = start_index + history_size if end_index is None: end_index = len(dataset) - target_size for i in range(start_index, end_index): indices = range(i-history_size, i, step) data.append(dataset[indices]) if single_step: labels.append(target[i+target_size]) targets.append(target_list[i+target_size]) else: labels.append(target[i:i+target_size]) targets.append(target_list[i:i+target_size]) return np.array(data), np.array(labels) ### 学習過程をグラフ化 def plot_train_history(history, title): loss = history.history['loss'] val_loss = history.history['val_loss'] epochs = [i for i in range(1, len(loss)+1)] plt.figure() plt.plot(epochs, loss, 'b', label='Training loss') plt.plot(epochs, val_loss, 'r', label='Validation loss') plt.ylim([0,1]) plt.xlabel('epochs') plt.ylabel(myloss) plt.title(title) plt.legend() plt.tight_layout() plt.savefig(title + '.png', dpi=300) plt.close() def create_time_steps(length): return list(range(-length, 0)) ### 折れ線グラフ化(シングルステップ) def single_step_plot(plot_data, delta, title, i): labels = ['History', 'True Future', 'Model Prediction'] marker = ['.-', 'rx', 'go'] time_steps = create_time_steps(plot_data[0].shape[0]) if delta: future = delta else: future = 0 plt.title(title + ': sample ' + str(i)) for i, x in enumerate(plot_data): if i: plot_data_y = plot_data[i] * data_std[objective_feature_index] + data_mean[objective_feature_index] plt.plot(future, plot_data_y, marker[i], markersize=10, label=labels[i]) else: plot_data_y = plot_data[i] * data_std[objective_feature_index] + data_mean[objective_feature_index] plt.plot(time_steps, plot_data_y.flatten(), marker[i], label=labels[i]) plt.legend() plt.xlim([time_steps[0], (future+5)]) plt.xlabel('Time-Step') plt.ylabel(features_considered[objective_feature_index]) plt.tight_layout() return plt ### 折れ線グラフ化(マルチステップ) def multi_step_plot(history, true_future, prediction, STEP, i): #plt.figure(figsize=(12, 6)) num_in = create_time_steps(len(history)) num_out = len(true_future) # 過去データ plot_data_y = np.array(history[:, objective_feature_index]) * data_std[objective_feature_index] + data_mean[objective_feature_index] plt.plot(num_in, plot_data_y, label='History') # 実際に起こったデータ plot_data_y = np.array(true_future) * data_std[objective_feature_index] + data_mean[objective_feature_index] plt.plot(np.arange(num_out)/STEP, plot_data_y, 'bo', label='True Future') # 予測データ if prediction.any(): plot_data_y = np.array(prediction) * data_std[objective_feature_index] + data_mean[objective_feature_index] plt.plot(np.arange(num_out)/STEP, plot_data_y, 'ro', label='Predicted Future') plt.xlabel('Time-Step') plt.ylabel(features_considered[objective_feature_index]) plt.legend(loc='upper left') plt.title('Multi Step Prediction: sample ' + str(i)) plt.tight_layout() plt.savefig('multi_step_plot_' + str(i) + '.png', dpi=300) plt.close() ### シングルステップモデル。未来を予測する def single_step_model_func(dataset): print('run -> single_step_model_func') # 訓練データ x_train_single, y_train_single = multivariate_data(dataset, dataset[:, objective_feature_index], 0, TRAIN_SPLIT, past_history, future_target, STEP, single_step=True) # バリデーションデータ x_val_single, y_val_single = multivariate_data( dataset, dataset[:, objective_feature_index], TRAIN_SPLIT, None, past_history, future_target, STEP, single_step=True) print ('Single window of past history : {}'.format(x_train_single[0].shape)) train_data_single = tf.data.Dataset.from_tensor_slices((x_train_single, y_train_single)) train_data_single = train_data_single.cache().shuffle(BUFFER_SIZE).batch(BATCH_SIZE).repeat() val_data_single = tf.data.Dataset.from_tensor_slices((x_val_single, y_val_single)) val_data_single = val_data_single.batch(BATCH_SIZE).repeat() # モデルの作成 single_step_model = tf.keras.models.Sequential() single_step_model.add(tf.keras.layers.LSTM(32, input_shape=x_train_single.shape[-2:])) single_step_model.add(tf.keras.layers.Dense(1)) single_step_model.compile(optimizer = myoptimizer, loss = myloss, metrics = ['accuracy']) # 学習過程をプリント表示 for x, y in val_data_single.take(1): print(single_step_model.predict(x).shape) single_step_history = single_step_model.fit(train_data_single, epochs = EPOCHS, steps_per_epoch = EVALUATION_INTERVAL, validation_data = val_data_single, validation_steps = VAL_STEPS) # 学習結果をグラフで表示 plot_train_history(single_step_history, 'Single Step Training and validation loss') i = 1 for x, y in val_data_single.take(5): single_step_plot([x[0][:, objective_feature_index].numpy(), y[0].numpy(), single_step_model.predict(x)[0]], 12, 'Single Step Prediction', i) plt.savefig('single_step_plot_' + str(i) + '.png', dpi=300) plt.close() i += 1 # 学習器を保存 single_step_model.save(now + 'single_step_model.h5') print(single_step_model.summary()) ### マルチステップモデル。未来を多変量(複数点範囲)で予測する def multi_step_model_func(dataset): print('run -> multi_step_model_func') x_train_multi, y_train_multi = multivariate_data(dataset, dataset[:, objective_feature_index], 0, TRAIN_SPLIT, past_history, future_target, STEP) x_val_multi, y_val_multi = multivariate_data( dataset, dataset[:, objective_feature_index], TRAIN_SPLIT, None, past_history, future_target, STEP) print ('Single window of past history : {}'.format(x_train_multi[0].shape)) print ('\n Target to predict : {}'.format(y_train_multi[0].shape)) train_data_multi = tf.data.Dataset.from_tensor_slices((x_train_multi, y_train_multi)) train_data_multi = train_data_multi.cache().shuffle(BUFFER_SIZE).batch(BATCH_SIZE).repeat() val_data_multi = tf.data.Dataset.from_tensor_slices((x_val_multi, y_val_multi)) val_data_multi = val_data_multi.batch(BATCH_SIZE).repeat() # モデルの作成 multi_step_model = tf.keras.models.Sequential() multi_step_model.add(tf.keras.layers.LSTM(units = 32, activation='tanh', recurrent_activation='hard_sigmoid', use_bias=True, kernel_initializer='glorot_uniform', recurrent_initializer='orthogonal', bias_initializer='zeros', dropout=0.0, recurrent_dropout=0.0, implementation=2, return_sequences=True, # 完全な系列を返すか kernel_regularizer=tf.keras.regularizers.l2(weight_decay), #kernel_regularizer=tf.keras.regularizers.l1_l2(l1=weight_decay, l2=weight_decay), input_shape=x_train_multi.shape[-2:])) multi_step_model.add(tf.keras.layers.LSTM(16, activation='relu')) multi_step_model.add(tf.keras.layers.Dense(future_target)) multi_step_model.compile(optimizer = myoptimizer, loss = myloss, metrics = ['accuracy']) # 学習過程をプリント表示 for x, y in val_data_multi.take(1): print (multi_step_model.predict(x).shape) multi_step_history = multi_step_model.fit(train_data_multi, epochs = EPOCHS, steps_per_epoch = EVALUATION_INTERVAL, validation_data = val_data_multi, validation_steps = VAL_STEPS) # 学習結果をグラフで表示 plot_train_history(multi_step_history, 'Multi-Step Training and validation loss') i = 1 for x, y in val_data_multi.take(5): multi_step_plot(x[0], y[0], multi_step_model.predict(x)[0], STEP, i) i += 1 # 学習器を保存 multi_step_model.save(now + 'multi_step_model.h5') print(multi_step_model.summary()) ### メイン関数 def main(): global target_list, data_mean, data_std tf.random.set_seed(7) # 乱数シードを指定(固定) features = df[features_considered] # 多変量(複数の特徴量)を元に解析する。リストで設定する target_list = list(df[target]) # インデックスをリスト化 features.index = df[target] # 横軸にする時系列データをPandasデータフレームでインデックスに設定 print(features.head()) # 解析するデータの最初の5行を目視確認 features.plot(subplots=False, grid=True) # グラフで確認 plt.savefig('features_plot.png', dpi=300) plt.close() dataset = features.values # 説明変数データをnumpy配列で抽出 data_mean = dataset[:TRAIN_SPLIT].mean(axis=0) # 平均値 data_std = dataset[:TRAIN_SPLIT].std(axis=0) # 標準偏差 dataset = (dataset-data_mean)/data_std # データを標準化 ### シングルテップモデル。未来の値ひとつを予測する single_step_model_func(dataset) ### マルチステップモデル。未来の値の範囲を予測する multi_step_model_func(dataset) ### パラメータの設定 if __name__ == '__main__': # テンソルフローのバージョンを表示 print('tensorflow ver', tf.__version__) # 読み出すcsvファイル csv_path = 'N225_10years_04_done.csv' # Pandasデータフレーム形式で読む df = pd.read_csv(csv_path) # 訓練データに使用する全体データの割合 train_ratio = 0.80 # 訓練データ数を計算 TRAIN_SPLIT = int(df.shape[0] * train_ratio) print('TRAIN_SPLIT:', TRAIN_SPLIT) # 時系列の列名 target = 'Date' # 複数列データから解析する場合 features_considered = ['Close', 'moving_average_5', 'moving_average_25', 'moving_average_75'] # 予測する目的変数のインデックスを指定 objective_feature_index = 1 # 予測する未来の数 future_target = 20 # 過去参照するデータ数:直近のこのデータ数分を元に、未来を予測する past_history = future_target * 3 # データ行をスキップする数。スキップしない場合は1(データをスキップせず使用する) STEP = 1 # バッチサイズ:一度に解析するデータの塊。 BATCH_SIZE = past_history print('BATCH_SIZE:', BATCH_SIZE) # 指定したバッファ(値)をシャッフルして得た番号で、バッチサイズ分を訓練データから抽出して解析する BUFFER_SIZE = int(TRAIN_SPLIT * train_ratio) #各世代の試行回数:「訓練データ÷バッチサイズ」の商以下が目安 EVALUATION_INTERVAL = TRAIN_SPLIT // BATCH_SIZE print('EVALUATION_INTERVAL:', EVALUATION_INTERVAL) #バリデーションの試行回数:「バリデーションデータ÷バッチサイズ」の商以下が目安 VAL_STEPS = (TRAIN_SPLIT*(1-train_ratio)/train_ratio) // BATCH_SIZE print('VAL_STEPS:', VAL_STEPS) # 学習する世代回数 EPOCHS = 10 # オプティマイザの設定 myoptimizer = tf.keras.optimizers.Adam(lr=0.001, # 学習率 beta_1=0.9, beta_2=0.999, epsilon=None, decay=0.0, amsgrad=False) # 指標とする損失関数 myloss='mean_absolute_error' # mean_squared_error mean_absolute_error # 重みの正則化 weight_decay = 1e-3 # メイン関数を実行 main() print('finished')
以上
<広告>