本記事では、PyCaretを用いてベストな回帰モデルを自動で作成する雛形コードと、作成した複数の回帰モデル(バイナリファイル)を利用して、Optunaを用いて多目的最適化を行う雛形コードを載せました。
最終的には、複数の目的変数に対して最小値or最大値を探索することで、下図のようにパレート解を取得します。csvファイルにも出力する仕様にしています。

例題として使用したデータは、機械学習の回帰分析用でお馴染みの「ボストンデータセット」です(下図例)。本来は、目的変数は「PRICE」でその他が説明変数です。しかし、本記事では多目的最適化の例とするためにもうひとつの目的変数として、「RM」の2つとしました。そして、説明変数は便宜上 ['LSTAT', 'PTRATIO', 'INDUS', 'DIS', 'AGE', 'CHAS']の6つとしました。

csvファイルとして作成する例は次のリンク先です。Python scikit-learn付属のボストン市の住宅価格データ(Boston house prices dataset)をcsvファイル化する - PythonとVBAで世の中を便利にする
◆以下、本コード実施例について説明します。
本コードを実行すると下図のようにヒストグラムを作成します。

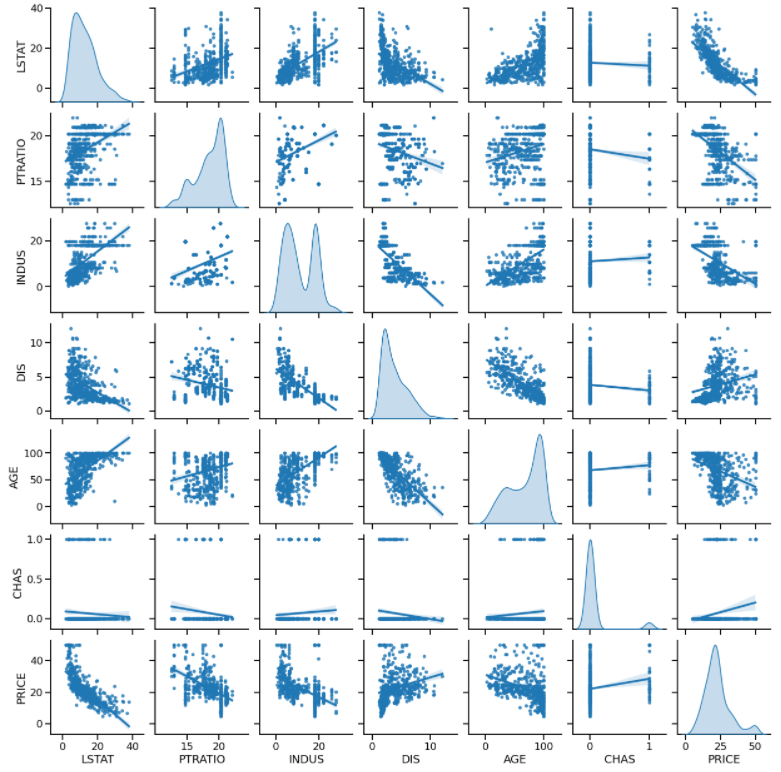
また、下図のように行列散布図を作成します。
そして、下図のようにして、ベストな回帰モデルを自動で選定します。

その結果、下図のように作成した回帰モデルの相関性を可視化します。

また、作成した回帰モデルの誤差も図示します。

更に、目的変数に対する感度の高い説明変数のランキングを作成します。

最終的には、下図のようにパレート解をcsvファイルで取得します。これを図示したのが冒頭のグラフです。

■本プログラム
▼PyCaretで回帰モデルを作成する
目的変数の数だけ回帰モデルを作成します。目的変数名はコード中の「target_name」で指定します。これを目的変数の数だけ実行して、回帰モデル「best_model_***.pkl」をバイナリファイルで作成します(***は目的変数名です)。
#!/usr/bin/env python # coding: utf-8 # In[1]: # データセットを読み込む import pandas as pd file_path = './boston_XYdata.csv' df = pd.read_csv(file_path, # csvファイルをpandasのDataFrame型で読み込む sep=',', skiprows=0, header=0, encoding='utf-8') print(df) # In[2]: # 回帰分析するために、必要な列を抽出する # 説明変数の列名 featrure_name_list = ['LSTAT', 'PTRATIO', 'INDUS', 'DIS', 'AGE', 'CHAS'] # 目的変数の列名 'PRICE' 'RM' target_name = 'PRICE' dataset_name_list = featrure_name_list.copy() dataset_name_list.append(target_name) print(dataset_name_list) df2 = df[dataset_name_list] print(df2) # In[3]: # 欠損値データの確認 print(df2.isna().sum()) # In[4]: # 欠損値がある行を削除する DF = df2.dropna() print(DF) # In[5]: # 基本統計量の確認 DF_describe = DF.describe().T DF_describe # In[6]: # ヒストグラムを作成する import matplotlib matplotlib.use('Agg') # バックグラウンドで画像生成などする宣言 from matplotlib import pyplot as plt DF.hist() plt.tight_layout() plt.savefig('graph_histogram_' + target_name + '.png') plt.close() # In[7]: # 行列散布図の作成 import seaborn as sns sns.set_context('talk') ax = sns.pairplot( DF, #y_vars = target_name, # y軸のカラム #hue = 'CHAS', # 凡例に表示したい列名を指定(カテゴリ変数) #palette = 'gnuplot2', # 'tab10' 'magma' 'cool' 'bar' 'gnuplot2' kind = 'reg', # 線形近似線を記入 markers = '.', diag_kind = 'kde', diag_kws = dict(shade = True), #height = 3, #aspect = 3/4 ) #ax.set(ylim=(0, 3)) # y軸の範囲(レンジ)を指定 plt.savefig('graph_pairplot_' + target_name + '.png') plt.close() # In[8]: # PyCaret用のデータセット生成(前処理) from pycaret.regression import * set_data = setup( data = DF, normalize = False, # 標準化するかどうか #normalize_method = 'zscore', # 標準化'zscore' 正規化'minmax' # 絶対値を1'maxabs' ロバスト'robust #ignore_features = ['ZN', 'CHAS', B'], train_size = 0.7, # 訓練データの割合 session_id = 1, # ランダムシード target = target_name, # 目的変数 categorical_features=['CHAS'], # カテゴリ型を指定する場合 numeric_features = ['LSTAT', 'PTRATIO', 'INDUS', 'DIS', 'AGE'], # 数値型を指定する場合 #remove_outliers = False, # 外れ値の除去 #outliers_threshold = 0.05, # 0.05の場合、分布の両端裾の0.025%を除去 #remove_multicollinearity = False, # マルチコ(多重共線性)除去 #multicollinearity_threshold = 0.9, # 強い相関のある説明変数の片方を削除する #create_clusters = False, # クラスタリングにより新規特徴量を作成するかどうか #cluster_iter = 20, # default 20 #polynomial_features = False, # 交互作用項を作成するか(新規特徴量) #trigonometry_features = False # 三角関数で作成するか #polynomial_degree = 2, # ↑次数で作成するか。[1, a, b, a^2, ab, b^2] #polynomial_threshold = 0.1, # 特徴量を残す判定しきい値 #feature_interaction = False, # 交互作用(a * b) #feature_ratio = False, # 交互作用(a / b) #interaction_threshold = 0.01, # 特徴量を残す判定しきい値 #pca = False, # 主成分分析による次元削減 #pca_method = 'linear', # 'linear' 'kernel' 'incremental' #pca_components = 0.99, # 残す特徴量数。int型では数を指定。float型は割合 silent=True, # 型チェックの手動確認のため一時ストップするか。ストップする場合False ) # In[9]: # モデルを比較してトップ5のモデルを抽出 top5 = compare_models(n_select = 5, sort = 'MAE', verbose = False) #default is 'R2' #MAE, MSE, RMSE, R2, RMSLE, MAPE # In[10]: # 各モデルのハイパーパラメータをデフォルト範囲で自動調整する tuned_top5 = [tune_model(i, verbose = False) for i in top5] # In[11]: # ベスト回帰モデルを自動で選定する best = automl(optimize = 'MAE') # モデルを評価する predict_model(best) # In[12]: # 相関性 plot_model(best, plot = 'error') plt.savefig('graph_error_' + target_name + '.png') plt.close() # In[13]: # 残渣 plot_model(best, plot = 'residuals') plt.savefig('graph_residuals_' + target_name + '.png') plt.close() # In[14]: # 特徴量の可視化 plot_model(best, plot = 'feature') plt.savefig('graph_feature_' + target_name + '.png') plt.close() # In[15]: # ハイパーパラメータの出力 plot_model(best, plot = 'parameter') plt.savefig('graph_parameter_' + target_name + '.png') plt.close() # In[16]: # 特徴量のサマリー try: interpret_model(best) plt.savefig('graph_interpret_model_' + target_name + '.png') plt.close() #interpret_model(best, plot = 'correlation') #interpret_model(best, plot = 'reason', observation = 0) except: pass # In[17]: # 回帰モデルを保存する save_model(best, model_name = 'best_model_' + target_name) # In[ ]:
▼Optunaによる多目的最適化でパレート解を取得する
上記コードで作成した複数の回帰モデル「best_model_***.pkl」を目的関数とします。Optunaの多目的最適化で、各々の最小値or最大値を探索します。
#!/usr/bin/env python # coding: utf-8 # In[1]: # PyCaret用の回帰モデルを読み込む from pycaret.regression import * target_y1_name = 'PRICE' target_y2_name = 'RM' load_model_y1 = load_model('best_model_' + target_y1_name) load_model_y2 = load_model('best_model_' + target_y2_name) print(load_model_y1) print(load_model_y2) # In[2]: import optuna import matplotlib matplotlib.use('Agg') # バックグラウンドで画像生成などする宣言 import matplotlib.pyplot as plt # 目的関数の定義。複数の目的変数を戻り値とする def objective(trial): # 指定範囲の乱数の生成 lstat = trial.suggest_float('LSTAT', 1.7, 38) # 変数lstatを上下限1.7~38の範囲で浮動小数点 ptratio = trial.suggest_float('PTRATIO', 12.6, 22) indus = trial.suggest_float('INDUS', 0.4, 24) dis = trial.suggest_float('DIS', 1.1, 12) age = trial.suggest_float('AGE', 3, 100) chas = trial.suggest_categorical('CHAS', ['0', '1']) # カテゴリ変数の場合 # 予測するデータセットの作成(データフレーム型) df = pd.DataFrame([(lstat, ptratio, indus, dis, age, chas)], columns= ['LSTAT', 'PTRATIO', 'INDUS', 'DIS', 'AGE', 'CHAS']) # 予測する predict_y1 = predict_model(load_model_y1, data=df).values.tolist()[0][-1] predict_y2 = predict_model(load_model_y2, data=df).values.tolist()[0][-1] return predict_y1, predict_y2 # 最適化の条件設定 study = optuna.multi_objective.create_study( directions=["minimize", "maximize"], # "minimize" "maximize" sampler=optuna.multi_objective.samplers.NSGAIIMultiObjectiveSampler(seed = 1) #sampler=optuna.multi_objective.samplers.RandomMultiObjectiveSampler(seed = 1) ) # 最適化の実行 study.optimize(objective, n_trials=200) # 最適化過程で得た履歴データの取得。get_trials()メソッドを使用 trials = {str(trial.values): trial for trial in study.get_trials()} trials = list(trials.values()) # グラフにプロットするため、目的変数をリストに格納する y1_all_list = [] y2_all_list = [] for i, trial in enumerate(trials, start=1): y1_all_list.append(trial.values[0]) y2_all_list.append(trial.values[1]) # パレート解の取得。get_pareto_front_trials()メソッドを使用 trials = {str(trial.values): trial for trial in study.get_pareto_front_trials()} trials = list(trials.values()) trials.sort(key=lambda t: t.values) # グラフプロット用にリストで取得。またパレート解の目的変数と説明変数をcsvに保存する y1_list = [] y2_list = [] with open('pareto_data.csv', 'w') as f: for i, trial in enumerate(trials, start=1): if i == 1: columns_name_list = ['trial_no', target_y1_name, target_y2_name] columns_name_str = ','.join(columns_name_list) data_list = [] data_list.append(trial.number) y1_value = trial.values[0] y2_value = trial.values[1] y1_list.append(y1_value) y2_list.append(y2_value) data_list.append(y1_value) data_list.append(y2_value) for key, value in trial.params.items(): data_list.append(value) if i == 1: columns_name_str += ',' + key if i == 1: f.write(columns_name_str + '\n') data_list = list(map(str, data_list)) data_list_str = ','.join(data_list) f.write(data_list_str + '\n') # パレート解を図示 plt.rcParams["font.size"] = 16 plt.figure(dpi=120) plt.title("multiobjective optimization") plt.xlabel(target_y1_name) plt.ylabel(target_y2_name) plt.grid() #plt.scatter(y1_all_list, y2_all_list, c='blue', label='all trials') #plt.scatter(y1_list, y2_list, c='red', label='pareto front')
plt.scatter(y1_all_list, y2_all_list, facecolor='None', edgecolors='blue', label='all trials')
plt.scatter(y1_list, y2_list, facecolor='None', edgecolors='red', label='pareto front')
plt.legend() plt.tight_layout() plt.savefig("pareto_graph.png") plt.close() # In[ ]:
以上
<広告>