本記事では、Pycaretを用いて、スタッキング(Stacking)回帰モデルを構築する雛形コードを載せました。概要は下記です。
# スタッキング stacked_model = stack_models(estimator_list = [reg], # 合成する回帰モデルをリストで指定。複数指定可 meta_model = best, # 土台となる回帰モデルを指定 choose_better = True, optimize = 'MAE')
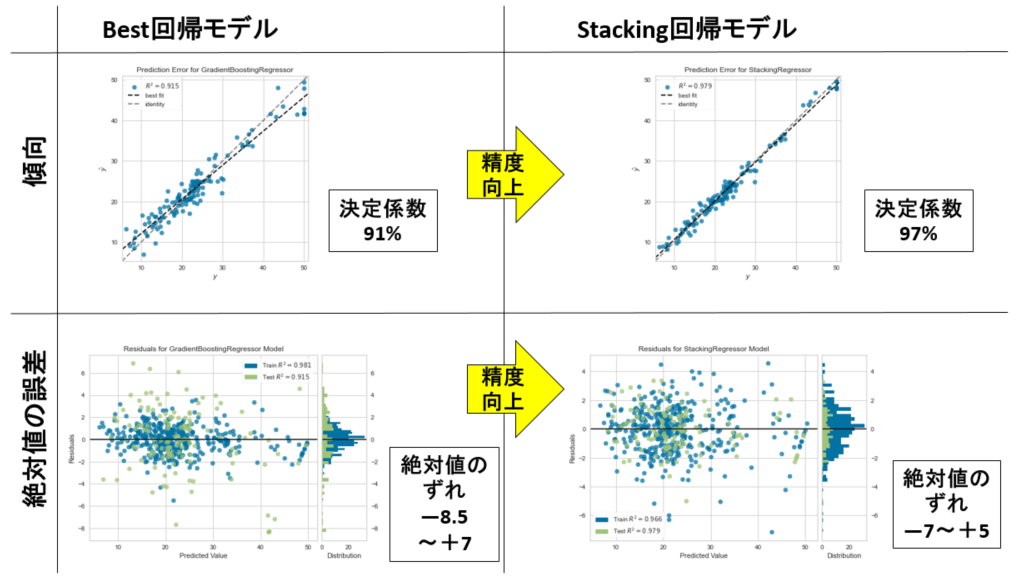
下図は、そのスタッキング回帰モデルの効果を示した図です。下図左は、Pycaretによるベスト回帰モデルの精度です。一方、下図右は、そのベスト回帰モデルとは別に線形回帰モデルを作成して、その2つを合成したスタッキング回帰モデルです。明らかに精度向上してる様子がわかります。つまり、未知の予測をしたい場合は、今回の場合、スタッキング回帰モデルが良いと判断できます。
■本プログラム
テストに用いたデータは、機械学習の回帰分析でお馴染みのボストンデータセットです。ググれば出てきます。
#!/usr/bin/env python # coding: utf-8 # In[1]: # データセットを読み込む import os import pandas as pd file_path = './boston_dataset.csv' df = pd.read_csv(file_path, # csvファイルをpandasのDataFrame型で読み込む sep=',', skiprows=0, header=0, encoding='utf-8') display(df) # In[2]: # PyCaret用のデータセット生成(前処理) from pycaret.regression import * set_data = setup(data = df, normalize = False, # 標準化するかどうか #normalize_method = 'zscore', # 標準化'zscore' 正規化'minmax' # 絶対値を1'maxabs' ロバスト'robust #ignore_features = ['ZN', 'CHAS', B'], train_size = 0.75, # 訓練データの割合 session_id = 1, # ランダムシード target = 'PRICE', # 目的変数 #categorical_features=['列名'], # カテゴリ型を指定する場合 #numeric_features = ['列名'], # 数値型を指定する場合 #remove_outliers = False, # 外れ値の除去 #outliers_threshold = 0.05, # 0.05の場合、分布の両端裾の0.025%を除去 #remove_multicollinearity = False, # マルチコ(多重共線性)除去 #multicollinearity_threshold = 0.9, # 強い相関のある説明変数の片方を削除する #create_clusters = False, # クラスタリングにより新規特徴量を作成するかどうか #cluster_iter = 20, # default 20 #polynomial_features = False, # 交互作用項を作成するか(新規特徴量) #trigonometry_features = False # 三角関数で作成するか #polynomial_degree = 2, # ↑次数で作成するか。[1, a, b, a^2, ab, b^2] #polynomial_threshold = 0.1, # 特徴量を残す判定しきい値 #feature_interaction = False, # 交互作用(a * b) #feature_ratio = False, # 交互作用(a / b) #interaction_threshold = 0.01, # 特徴量を残す判定しきい値 #pca = False, # 主成分分析による次元削減 #pca_method = 'linear', # 'linear' 'kernel' 'incremental' #pca_components = 0.99, # 残す特徴量数。int型では数を指定。float型は割合 silent=True, # 型チェックの手動確認のため一時ストップする場合はFalse ) # In[3]: # モデルを比較してトップ3のモデルを抽出 top3 = compare_models(n_select = 3, sort = 'MAE', #default is 'R2' MAE, MSE, RMSE, R2, RMSLE, MAPE verbose = False) # In[4]: # 各モデルのハイパーパラメータをデフォルト範囲で自動調整する tuned_top3 = [tune_model(i, verbose = False) for i in top3] # In[5]: # ベスト回帰モデルを自動で選定する best = automl(optimize = 'MAE') # In[6]: # モデルを評価する predict_model(best) # In[7]: # 結果の可視化 plot_model(best, plot = 'error') # In[8]: # 残渣 plot_model(best, plot = 'residuals') # In[9]: # 線形回帰分析 reg = create_model('ridge') # lr, ridge # In[10]: # スタッキング stacked_model = stack_models(estimator_list = [reg], # 合成する回帰モデルをリストで指定。複数指定可 meta_model = best, # 根幹となる回帰モデルを指定 choose_better = True, optimize = 'MAE') # In[11]: # 合成した回帰モデルをファイナライズする final_model = finalize_model(stacked_model) # In[12]: plot_model(estimator = final_model, plot = 'error') # In[13]: # 残渣 plot_model(final_model, plot = 'residuals') # In[14]: predict_model(final_model) # In[15]: # 回帰モデルを保存する import datetime now = datetime.datetime.now() now = now.strftime("%y%m%d") save_model(final_model, model_name = 'finale_model_' + now) # In[16]: # 保存した回帰モデルをロードする load_reg_model = load_model('finale_model_' + now) # In[17]: # 新しいデータを読み込んで予測する(ここでは、便宜上、訓練データとテストデータを全部読み込む) predict_df = predict_model(load_reg_model, data=df) display(predict_df) # In[18]: # 適合度(相関性)をグラフで確認する。 import matplotlib.pyplot as plt import numpy as np from scipy import optimize import math ### 近似式 y = ax 用の関数 def approximation_expression(x, a): return a * x # 相関性の確認 横軸Y:縦軸Pred_Y def plot_reg(DF, target_Yname, pred_Yname): Y = DF[target_Yname].values.tolist() # 生データをリストへ格納 pred_Y = DF[pred_Yname].values.tolist() # 予測結果をリストへ格納 # 近似式の作成 popt, pcov = optimize.curve_fit(approximation_expression, Y, pred_Y) ax = plt.figure(num=0, dpi=120).gca() #plt.rcParams["axes.labelsize"] = 15 ax.set_title("pred vs real ", fontsize=14) ax.set_xlabel(target_Yname, fontsize=14) ax.set_ylabel("Pred\n" + target_Yname, fontsize=14) rp = ax.scatter(x = target_Yname, y = pred_Y, data = DF, facecolors="none", edgecolors='black') # purple # 生データの最小値と最大値 y_min = DF[target_Yname].min() y_max = DF[target_Yname].max() # 予測データの最小値と最大値 y_pred_min = DF[pred_Yname].min() y_pred_max = DF[pred_Yname].max() # プロットするためのxデータの範囲を決める x_min = min(y_min, y_pred_min) x_max = max(y_max, y_pred_max) # グラフのレンジを決める x_range = x_max - x_min # データの範囲が100以下か以上かで分ける print("x_range = x_max - x_min = " + str(x_range)) if x_max > 1: print("range A") min_lim = 0 if x_range <= 10: max_lim = math.floor(x_max + 1) else: max_lim = math.floor(x_max + 10) elif x_max >= 0: print("range B") min_lim = -0.1 max_lim = 1.1 elif x_min >= -1: print("range C") min_lim = -1.1 max_lim = 0.1 else: print("range D") max_lim = 0.1 if x_range <= 100: min_lim = math.floor(x_min - 1) else: min_lim = math.floor(x_min - 10) print(min_lim, max_lim) rp.axes.set_xlim(min_lim, max_lim) rp.axes.set_ylim(min_lim, max_lim) # 近似式プロットのためのデータを作成 x_approximation = np.linspace(min_lim, max_lim, 10) # numpyでxデータを作成 y_approximation = popt[0] * x_approximation # 近似式に代入してyデータを作成 line_approximation = ax.plot(x_approximation, y_approximation, linestyle = 'dashed', linewidth = 3, color='r') rp.axes.set_aspect('equal', adjustable='box') plt.grid(True) # 凡例を指定して記入する場合は、リストで指定する ax.legend([line_approximation[0]], ["y = {:.3f}x".format(popt[0])], loc='upper left', numpoints=1, fontsize=14) plt.tick_params(labelsize=14) plt.tight_layout() plt.show() #plt.savefig(now + '_real_vs_pred.png') #plt.close() plot_reg(predict_df, 'PRICE', 'Label') # In[19]: # 予測結果をファイルに保存する predict_df.to_csv(now + '_predict.csv', index=False, encoding='utf-8') # In[ ]:
以上
<広告>
リンク