Python 「PyCaret」ベストな回帰モデルを自動選定するautoml()

'23/04/15更新：先日、PyCaretがver3.0.0（3系）にアップしたのを機会に、雛形コードを刷新しました。そして、次のGithubへ載せました。

template_for_regression_analysis_using_pycaret3/template_for_regression_using_pycaret3.ipynb at main · hk29-ai/template_for_regression_analysis_using_pycaret3 · GitHub

本記事では、上記コードの説明をグラフ付きでしています。PyCaretの利点は、わずか一行のコードで、世の中にある線形、非線形の回帰モデル20個ほどを順番に実行して、その予測精度結果を元に、回帰モデルのランキングを作成することです（下図）。

そのコードは下記です。
top3 = compare_models(n_select = 3, sort = 'MAE') # R2, MAE, MSE, RMSE, R2, RMSLE, MAPE

引数sortは、回帰モデルのランキングを作成する精度の指標です。そして、n_selectで3を指定してることで、トップ3の回帰モデルをリストで抽出しています

次に、下記コードでトップ3の各回帰モデルのハイパーパラメータを自動調整して再度回帰モデルを生成します。

tuned_top3 = [tune_model(i) for i in top3]

そして、次のようにautomlでベスト回帰モデルを自動で選定します。
best = automl(optimize = 'MAE')

回帰モデルは作成するだけでなくて、その予測精度を確認することが重要です。下図は、横軸が元データで、縦軸が作成した回帰モデルによる予測結果です。y=xの比例線上に乗って右肩あがりであれば、データの傾向の再現性は高いと言えます。

下図は、作成した回帰モデルの予測精度の絶対値のずれ量を確認するためのグラフです。横軸は、回帰モデルによる予測結果で縦軸は元データとのずれ量です。青色が訓練データで、緑色がテストデータによる結果です。下図の場合、予測精度の絶対値のずれ量は、最大で－6～5.8程のずれ量が少なくともあり得る精度の回帰モデルと言えます。

以下では、回帰モデル作成（回帰分析）によって得られた結果をグラフ化してゆきます。Pythonライブラリのshapを用いています。線形、非線形、合成回帰モデルの結果に対して実行できます。

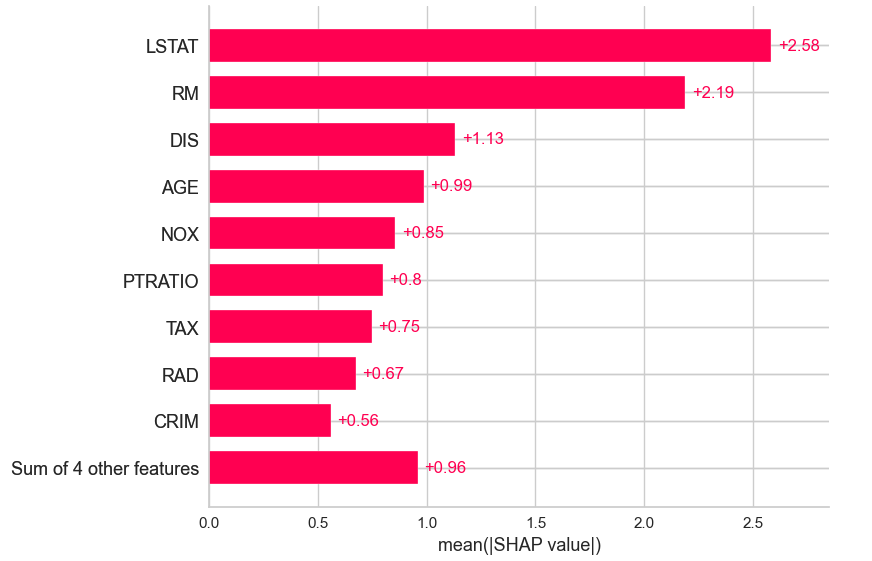
下図は、シャープレイ値を指標に、目的変数に対する感度の高い特徴量（説明変数）のランキングを図示したグラフです。上位から順にLSTAT、RM、DIS、AGEとわかります。

下図も同様な特徴量のランキングで、さらに細かい情報を図示しています。横軸は目的変数に対する影響度（シャープレイ値）、縦軸は各説明変数です。赤色から青色は説明変数(Feature)が大きい、小さい場合に対応します。例えば、RMは部屋数を表し、その赤点が右側に多くプロットされています。このことより、部屋数が多い程、目的変数である住宅価格が高くなる傾向であると理解することが出来ます。